ریاضیات همه جا هست

اگر با دقت به اطراف نگاه کنیم

ریاضیات همه جا هست

تراشه چوب و رابطه ی آن با منحنی مارپیچ ارشمیدس

10 راهکار برای رفع خواب آلودگی و خستگی هنگام درس خواندن

تقارن در خلقت

پروانه زیبایی که ۸۹-۹۸ نام دارد .

🔸تقارن در خلقت🔸

🔹نقش روی بال های این پروانه ، عدد ۸۹-۹۸ را نشان می دهد،

به همین دلیل او را به این اسم نامگذاری کرده اند.

 

حاصل ترکیب دو علم ریاضی و فیزیک

چگونه ریاضیات را بهتر فرا بگیریم؟

برخی از دانش آموزان نسبت به درس ریاضیات دیدگاه خوبی ندارند و تصور می کنند ریاضیات جزو دروس سخت و پیچیده است و نمی توان به آسانی ریاضیات را فرا گرفت! اما واقعیت این است که ریاضیات هم مانند بقیه دروس تکنیک ها و روش های خاص خود را برای فراگیری بهتر دارد.

جالب است بدانید که بعضی از دانش آموزان، ریاضیات را مانند تاریخ و جغرافی و تعلیمات اجتماعی، می خوانند!

خواندن ریاضیات همان‌قدر خنده دار است که حل و تمرین جغرافیا!

اما باید بدانیم که ریاضیات خواندنی نیست و تنها و بهترین راه حل برای فراگیری صحیح ریاضیات، حل مسئله است.

در واقع تکرار در حل مسائل مختلف می تواند باعث مهارت در ریاضیات شود.

اگر شما هم جزو دانش آموزانی هستید که نحوه صحیح فراگیری ریاضیات را بلد نیستید، به این چند نکته توجه کنید:

1- ابتدا جزوه یا متن آموزشی که در اختیارتان هست را نگاه کنید و‌ مطالب آن را به خاطر بسپارید. سعی کنید مفاهیمی که مدنظر است را یاد بگیرید.

2- سؤالات، تمارین و مسائلی که مرتبط با آن مفهوم است را از ساده به سمت دشوار حل کنید. اگر در ابتدا برایتان این کار مشکل است، پاسخ سؤالات را نگاه کنید و سعی کنید استراتژی حل مسئله را یاد بگیرید.

3- رفته رفته سعی کنید به پاسخ ها نگاه نکنید و خودتان مسائل را حل کنید. یادتان باشد که تمرین و تکرار زیاد در حل مسائل آسان، متوسط و دشوار، شما را حرفه ای خواهد کرد.

4- از مطالبی که مرور کردید و‌ تمارینی که حل کردید،  مانند یک جلسه امتحان واقعی از خودتان آزمون بگیرید و اشکالات خود را بیابید.

5- حال وقت تمرین مجدد و وقت گذاری بر روی نقاط ضعف است. مجدد بر روی نقاط ضعفتان متمرکز شوید و مسائل متنوع تر و بیشتری حل کنید.

6- مجدد یک نگاه سطحی بر روی جزوه تان و مسائلی که حل کردید بیندازید و پس از یک‌ ساعت مجدد از خودتان امتحان بگیرید.

7- یادتان باشد که اگر باز هم اشکالاتی داشتید باید باز هم برگردید و با تمرین بر روی آن مبحث، تسلط خود را افزایش دهید.

8- اگر کاملا بر روی تمام مباحث تسلط داشتید، به یاد داشته باشید که مرور و تمرین مجدد در روز های آینده، باعث تثبیت مطالب آموخته شده توسط شما خواهد شد.

 

محاسبه مساحت کره زمین

زاویه دید

مدل هندسی بال زدن پرندگان

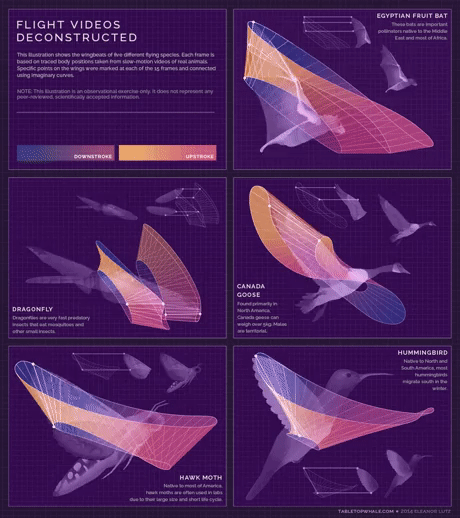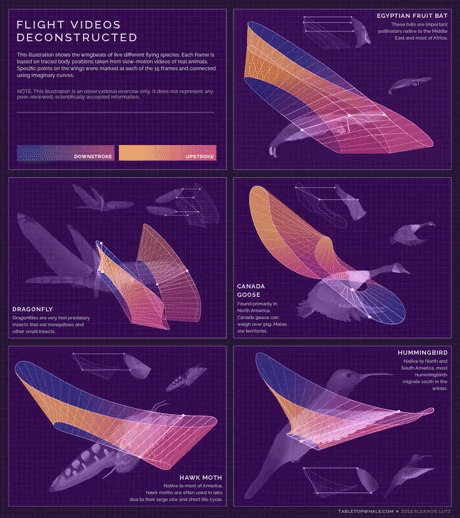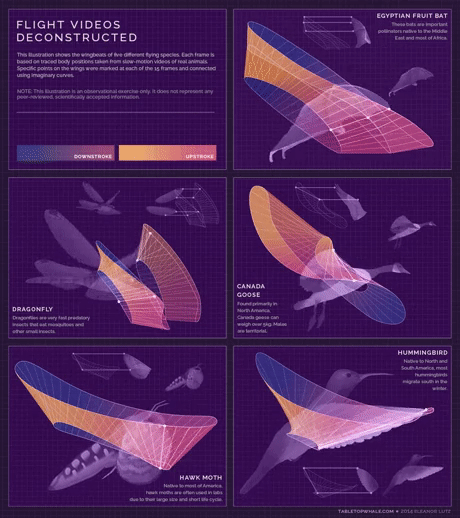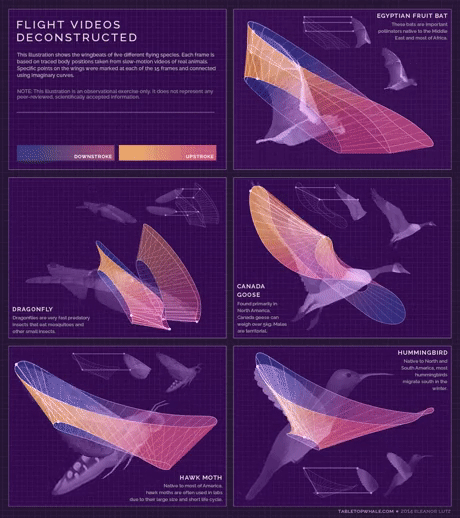
مدل هندسی

بال زدن پنج پرنده

به ترتیب خفاش سنجاقک ، غاز کانادایی ، شب پره و مرغ مگس خوار

 

نرم افزار جئوجبرا ( GeoGebra )

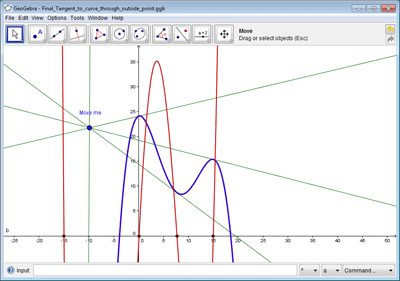
Geogebra محصول تیم متخصص با پشتیبانی دانشگاه سالزبورگ اتریش نرم افزار جامعی مربوط به مباحث حساب، جبر و هندسه است. در این برنامه محیط ترسیم اشکال هندسی، محیط ورود فرمان های ریاضی و ناحیه اطلاعات جبری در نظر گرفته شده است. ظاهر نرم افزار بسیار جذاب و هوشمند بوده و کلیه امکانات برای بررسی های تحلیلی و ترسیمی را فراهم می آورد. خروجی جاوا اپلت این نرم افزار بدون نقص به همراه گزینه های فراوانی است.

نرم افزار GeoGebra در مقایسه با دیگر نرم افزارها از لحاظ توانمندی های ترسیمی، ظاهر، وسعت عمل، محتوای آموزشی برای معلمین و دانش آموزان، ارتباط با کاربران، خروجی جاوا و بروز بودن مناسب ترین نرم افزار محسوب می شود.

دسرهای هندسی

تکنیک هایی برای جلوگیری از خستگی و حفظ انگیزه ی مطالعه

🖍 از مداد و خودکارهای رنگی استفاده کنید.

🗒 روی برچسب های کاغذی یادداشت کنید.

⏰ بعد از 45 دقیقه مطالعه، یک استراحت 15 دقیقه ای داشته باشید.

🎥 برای مطالب درسی به دنبال ویدئوهای آموزشی باشید.

☎️ با دوستانتان در مورد مطالب درسی گپ بزنید.

✍🏻 برای جلوگیری از خستگی، گاهی بخوانید و گاهی بنویسید.

🚶🏿 محل مطالعه را هر از چندی تغییر دهید.

✅ یک چک لیست از کارهایی که باید انجام دهید یا مطالبی که باید بیاموزید تهیه کنید و آن را علامت بزنید.

شش مسئله ی حل نشده ریاضی در عین ساده بودن صورتشان

۱. حدس کولاتز
یک عدد طبیعی انتخاب کنید؛ اگر زوج بود آن را بر ۲ تقسیم کنید و اگر فرد بود آن را ۳ برابر کنید و با ۱ جمع ببندید؛ برای عدد جدید به‌دست‌آمده همین فرایند را تکرار کنید؛ اگر این کار را ادامه دهید، در نهایت به عدد ۱ خواهید رسید؛ به‌عنوان مثال:
۷→۲۲→۱۱→۳۴→۱۷→۵۲→۲۶→۱۳→۴۰→۲۰→۱۰→۵→۱۶→۸→۴→۲→۱
این موضوع در سال ۱۹۳۷ توسط لوتار کولاتز مطرح شد و کماکان بعد از گذشت چندین دهه، حلی برای آن در دسترس نیست. درستی این حدس تا عدد ۲۶۰ توسط کامپیوتر بررسی شده است؛ اما هنوز اثباتی برای آن وجود ندارد

۲. اعداد اول دو‌‌قلو
همان‌طور که می­‌دانید عدد اول، عددی است که تنها بر ۱ و خودش بخش‌پذیر باشد. اعداد اولی که با همدیگر ۲ واحد اختلاف دارند، اعداد اول د‌و‌قلو نامیده می­‌شوند؛ مانند (۳٬۵) یا (۱۱٬۱۳).
بزرگ‌ترین اعداد اول دو‌قلوی کشف‌شده  که دارای ۳۸۸,۳۴۲ رقم هستند
این اعداد در سپتامبر ۲۰۱۶ کشف شدند. تعداد جفت‌های اعداد دوقلو تا عدد ۱۰۱۸ برابر است با ۸۰۸۶۷۵۸۸۸۵۷۷۴۳۶ . آیا تعداد اعداد اول دوقلو نامتناهی است؟ سؤالی که تاکنون بی‌پاسخ مانده است. اعداد اول سه‌قلو به سه عدد فرد متوالی گفته می‌شود که هر سه‌ی آن‌ها اول باشند؛ تنها اعداد اول سه‌قلو (۳٬۵٬۷) هستند، چرا؟

۳. حدس گلدباخ
یکی از معروف‌ترین و قدیمی‌ترین مسائل حل‌نشده در ریاضیات، حدس گلدباخ است که با وجود صورت بسیار ساده‌ای که دارد، حدود ۲۷۰ سال ذهن ریاضیدان‌ها را به خود مشغول کرده است. آرزوی هر ریاضیدانی این است که آن را حل کند و چه‌بسا برای رسیدن به حل آن همچون فیلم «اتاق فِرما» دست به هر کاری بزنند! حدس گلدباخ بیان می­‌کند که «هر عدد صحیح زوج بزرگ‌تر از ۲ را می‌توان به‌صورت مجموع دو عدد اول نوشت.» به‌عنوان مثال:
۴=۲+۲
۶=۳+۳
۸=۵+۳
این حدس در سال ۱۷۴۲ میلادی توسط کریستین گلدباخ در نامه‌ای به لئونارد اویلر مطرح شد. تلاش‌­های بسیاری در اثبات این حدس انجام شده است؛ تلاش‌هایی که منجر به کشف قضیه‌های دیگر شده‌اند؛ اما این حدس کماکان حل‌نشده باقی مانده است. در سال ۱۹۹۲ مؤسسه‌ی انتشاراتی مشهور Faber & Faber کتاب داستان پرفروشی با عنوان «عمو پتروس و حدس گلدباخ» منتشر کرد که در آن، تاریخ ریاضیات در قالبی جذاب و داستانی شرح داده شده است. بعد از چند سال، انتشارات مزبور به منظور تبلیغ برای فروش بیشتر، جایزه‌ای یک میلیون دلاری برای کسی که از تاریخ ۲۰ مارس  ۲۰۰۰ ،حداکثر به مدت دو هفته موفق به اثبات حدس گلدباخ شود، تعیین کرد؛ اما تا اتمام تاریخ مقرر و پس از آن، تاکنون هنوز هیچ ریاضیدانی از پس اثبات این حدس به‌ظاهر آسان، برنیامده است. در سال ۲۰۱۴ توسط کامپیوتر نشان داده شد که این حدس برای اعداد زوج کوچک‌تر از ۱۰۱۸×۴ درست است؛ اما هر چقدر این بررسی جلو برود، کافی نخواهد بود و در انتها تنها چاره‌ی ما تلاش برای اثبات آن است.

۴. اعداد کامل
دکارت گفت «اعداد کامل همچون انسان‌های کامل، کمیاب هستند.» عدد کامل عددی است که برابر جمع مقسوم‌علیه‌های به غیر خودش باشد؛ به‌عنوان مثال مقسوم‌علیه‌های ۶ به غیر خودش؛ ۱،۲،۳ هستند و داریم: ۶=۳+۲+۱. چند عدد کامل ابتدایی عبارتند از: ۲۸؛ ۴۹۶؛ ۸۱۲۸؛ ۳۳۵۵۰۳۳۶.
در ژانویه‌ی سال ۲۰۱۶، چهل‌ و ‌نهمین عدد کامل کشف شد؛ این عدد دارای ۴۴,۶۷۷,۲۳۵ رقم است.
از ویژگی‌های جالب اعداد کامل این است که آن‌ها را می‌توان به‌صورت جمع اعداد طبیعی متوالی یا جمع مکعب اعداد فرد متوالی نوشت. همچنین هر عدد کامل زوج، حتما به ۶ یا ۸ ختم می‌شود.
همچنان این سؤال‌ها که «آیا عدد کامل فرد وجود دارد؟» و «آیا تعداد اعداد کامل نامتناهی است؟» بی‌پاسخ مانده‌اند.
به نظر شما آیا عددی وجود دارد که مساوی با دو برابر جمع مقسوم‌علیه‌های به غیر از خودش باشد؟ نترسید! این سؤال حل شده است و پاسخش را به عهده‌ی خودتان می‌گذاریم. به این عدد، عدد کامل از مرتبه‌ی سه گفته می‌­شود.

۵. حدس لژاندر
این حدس بیان می‌کند «بین مجذور هر دو عدد طبیعی متوالی، حداقل یک عدد اول وجود دارد». این مسئله در سال ۱۹۱۲ توسط لژاندر بیان شد و حدود صد سال است که برای آن اثباتی پیدا نشده است. جالب است بدانید حل این حدس اگرچه منجر به حل فرضیه ریمان نمی‌­شود؛ اما قوی‌تر از یکی از نتایج فرضیه‌ی ریمان است.

۶. گنگ بودن π+e و πe

همان‌طور که می‌دانید به عددی گنگ گفته می‌شود که نتوان آن را به‌صورت کسری نوشت یا به عبارت ساده‌­تر؛ وقتی به‌صورت اعشاری نوشته شود، دارای الگوی مشخصی نباشد. اثبات گنگ بودن عددی مانند رادیکال ۲ راحت است. اما در حالت کلی اثبات گنگ بودن یک عدد، مسئله‌ی سختی به شمار می‌رود؛ به‌عنوان مثال اثبات گنگ بودن عدد پی در قرن ۱۸ توسط لمبرت و بعد از  اثبات گنگ بودن عدد نپر اتفاق افتاد. اما تاکنون اثبات نشده است که π+e و  πe گنگ هستند یا خیر.

عدد پی تا یک میلیون رقم اعشار

می توانید عدد پی را در بسته های ۱۰۰۰ رقم اعشار، ۵۰۰۰ رقم اعشار، ۱۰۰۰۰ رقم اعشار، ۲۵۰۰۰ رقم اعشار، ۵۰۰۰۰ رقم اعشار و ۱ میلیون رقم اعشار دانلود کنید .

برای دانلود روی تصویر زیر کلیلک کنید .

کاربرد هندسه

هنر دست ها و اشکال زیبای هندسی

 برای دیدن بهتر و راحت تر آن ، می توانید تصویر gif را ذخیره کرده و سپس به تماشای آن بنشینید .

میزان یادگیرى در حالت هاى متفاوت

میزان یادگیرى در حالت هاى متفاوت

10% وقتى می خوانیم

20% وقتى می شنویم

30% وقتى می بینیم

50% وقتى می بینیم و می شنویم

70% وقتى بحث می کنیم

80% وقتى تجربه می کنیم

95% وقتى به دیگران یاد می دهیم

وقتی یک ریاضیدان عاشق می شود !

تا چه عددی بلدی بشماری ؟!

 

تلفیق ریاضی و مهندسی

دنباله های اعداد

 

 

 

صدای عدد پی با آلات موسیقی

 " نواختن عدد پی با آلات موسیقی "

ثبت صدای عدد پی تا 122 رقم اعشار

 

بشنوید و از زیبایی ریاضی لذت ببرید .

 

برای دانلود روی تصویر کلیک کنید .

به بزرگی خودتان ایمان داشته باشید ...

مساحت و نمودار عشق

عـــشــــق

مساحت مشخصی ندارد

گاهی به اندازه

یک دل است و گاهی

به بزرگی یک دنیا

یاد بگیریم

با دل کوچکمان یک دنیا

عـــــشـــق بورزیـــــم

 

 

ریاضی و دنیای اطراف ما

روزگاری می گفتند ریاضی وسیله ای برای علوم دیگر است

ولی الان همه چیز ریاضی شده است،

فیزیک، اقتصاد، جامعه شناسی، ریاضی شده اند،

علم ریاضی شده است ....

 

( پروفسور رضا داوری اردکانی)

روی تصویر بالا کلیک کنید و رابطه ی زیبای بین ریاضی و دنیای اطراف ما را ببینید.

 

خطای دید

کودکانی که از هوش ریاضی – منطقی برخوردارند

کودکانی که از هوش ریاضی – منطقی برخوردارند :

🔸 1- دروس ریاضی و علوم را بر دیگر دروس مدرسه ترجیح می دهند .
🔸 2- ازشرکت در مسابقه هایی که موضوع آنها حل معما یا مساله ای باشد که به تفکر منطقی نیاز داشته باشد خوشحال می شوند .
🔸 3- از باز آفرینی آزمایش ها و تجارب علمی که در مدرسه یا فیلم های علمی از آن ها مطلع می شود لذت می برد . مثلا : شخصا آزمایش نقش نور - آب و هوا در ریشه ی گیاه را درمنزل بازسازی می کنند .
🔸 4- به خرید وسایل آزمایشگاهی و علمی مانند: ذره بین – میکروسکوپ و غیره و تشکیل یک آزمایشگاه خانگی در منزل علاقه مند هستند.
🔸5- ازشنیدن و دنبال کردن و انتقال دادن اطلاعات در مورد آخرین دستاوردهای علمی ، پزشکی ، الکترونیکی و ریزپردازهای کامپیوتری و نرم افزاری – سخت افزاری .....لذت می برند.
🔸 6- چرا؟ چگونه ؟ چطور ؟ کلمه های پرسشی هستند که بسامد فراوانی در کلام او دارند و سؤالاتی مثل : چه میشد اگر ......؟؟؟
🔸 7- رفتن به موزه های فن آوری ، تاریخ فن آوری – طبیعی  ، نمایشگاه های کامپیوتری و نرم افزاری از موضوعات مورد علاقه ی آنهاست .
🔸 8- بازی های کامپیوتری مخصوصا آنهایی که نیاز به پیدا کردن راه حل و یا کشف راه های گوناگون دارد مثل ، پیدا کردن یک گنج مخفی به کمک نشانه ها، علامت ها ، اعداد و .... مانند بازی “ Never hood" لذت می برد .
🔸 9 - از بازی شطرنج و انواع بازی های فکری لذت می برد .
🔸 10- از طبقه بندی هر موضوعی لذت می برد و اصولا یکی از راه های به خاطر سپردن و فهمیدن موضوعات طبقه بندی و دسته بندی آنهاست . مثلا اگر تعدادی کلمه های مختلف ، از نظر رنگ ، اندازه ، جنس ، تعداد سوراخ ........ به او بدهید و از او بخواهید که آنها را از جنبه های مختلف دسته بندی کند ، شاید دانش آموزان دیگر همه را فقط در زیر یک عنوان دکمه ببینند درحالی که او  ،چندین دسته و طبقه و دسته های فرعی از آنها استخراج می کند.
🔸 11- ازخواندن یا دیدن فیلم های مربوط به زندگی نامه ی دانشمندان لذت می برند .
🔸 12- از رفتن به آسمان نماها و مطالعه درباره ی نجوم و کهکشان ها لذت می برند .
🔸 13- از دیدن فیلم های کمدی مثل پت و مت pat and mat  که موضوع آن نشان دادن کودنی شخصیت ها در حل مسایل است لذت می برد .
🔸 14- از کدگذاری شخصی یا کشف کدهایی که می بیند مثل علایم راهنمایی و رانندگی – شماره ی پلاک ماشین ها .....خوشش می آید و برای به خاطرسپردن اسامی متعدد یک مجموعه، از کدگذاری استفاده می کند . مثلا برای به خاطرسپردن اسامی شهرهای یک استان از ساختن یک کلمه با حرف اول شهرهای مورد نظر کلمه ای می سازد که بتواند بعدا آنها را به یاد بیاورد .
❣ مستعد در رشته های زیر :
 علوم پایه به ویژه ریاضی، مهندسی، حسابداری، برنامه‌نویسی کامپیوتر، متخصص فلسفه مخصوصا فلسفه علم و مجری طرح‌های پژوهشی .

 

روشی ساده برای بخاطر سپردن اندازه ی نسبت های مثلثاتی زوایا

مثلثی با سه زاویه ی 90 درجه!

جادوی عدد 9

زیبایی های ریاضی درروابط ریاضی وترسیم های هندسی مختصاتی

زیبایی های ریاضی در روابط ریاضی و ترسیم های هندسی مختصاتی

در قالب فایل های فلش زیبا ، جالب و دیدنی

در ادامه ی مطلب

 

 

ادامه نوشته